Advertisements
Advertisements
प्रश्न
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that: (i) ΔAOB and ΔCOD (ii) If OA = 6 cm, OC = 8 cm,
Find:(a) `("area"(triangleAOB))/("area"(triangleCOD))`
(b) `("area"(triangleAOD))/("area"(triangleCOD))`
उत्तर
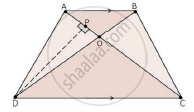
We have,
AB || DC
In ΔAOB and ΔCOD
∠AOB = ∠COD [Vertically opposite angles]
∠OAB = ∠OCD [Alternate interior angles]
Then, ΔAOB ~ ΔCOD [By AA similarity]
(a) By area of similar triangle theorem
`("area"(triangleAOB))/("area"(triangleCOD))="OA"^2/"OC"^2=6^2/8^2=36/64=9/16`
(b) Draw DP ⊥ AC
`therefore("area"(triangleAOD))/("area"(triangleCOD))=(1/2xxAOxxDP)/(1/2xxCOxxDP)`
`="AO"/"CO"=6/8=3/4`
APPEARS IN
संबंधित प्रश्न
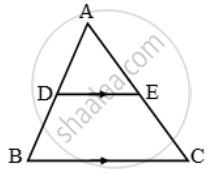
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals
In figure below ΔACB ~ ΔAPQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm,
find CA and AQ. Also, find the area (ΔACB): area (ΔAPQ)

Triangles ABC and DEF are similar If AB = 1.2 cm and DE = 1.4 cm, find the ratio of the areas of ΔABC and ΔDEF.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
The areas of two similar triangles are 25 cm2 and 36 cm2 respectively. If the altitude of the first triangle is 2.4 cm, find the corresponding altitude of the other.
If ΔABC and ΔBDE are equilateral triangles, where D is the mid-point of BC, find the ratio of areas of ΔABC and ΔBDE.
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
In the given figure, ΔACB ~ ΔAPQ. If AB = 6 cm, BC = 8 cm, and PQ = 4 cm then AQ is equal to ______.
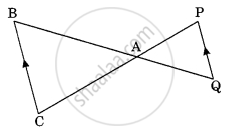
If ΔPQR ∼ ΔABC; PQ = 6 cm, AB = 8 cm and the perimeter of ΔABC is 36 cm, then the perimeter of ΔPQR is ______.
