Advertisements
Advertisements
प्रश्न
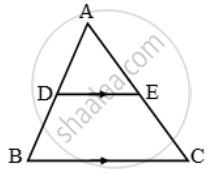
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
उत्तर
∆ADE ~ ∆ABC.
`\therefore \frac{ar(\Delta ADE)}{ar(\Delta ABC)}=(DE^2)/(BC^2)=((DE)/(BC))^2=(3/5)^2=9/25`
Let ar (∆ADE) = 9x sq units
Then, ar (∆ABC) = 25x sq units
ar (trap. BCED) = ar (∆ABC) – ar (∆ADE)
= (25x – 9x) = (16x) sq units
`\therefore \frac{ar(\Delta ADE)}{ar(trap.BCED)}=\frac{9x}{16x}=\frac{9}{16}`
APPEARS IN
संबंधित प्रश्न
The areas of two similar triangles ∆ABC and ∆PQR are 25 cm2 and 49 cm2 respectively. If QR = 9.8 cm, find BC
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
Triangles ABC and DEF are similar If AB = 1.2 cm and DE = 1.4 cm, find the ratio of the areas of ΔABC and ΔDEF.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
The areas of two similar triangles are 25 cm2 and 36 cm2 respectively. If the altitude of the first triangle is 2.4 cm, find the corresponding altitude of the other.
In ΔABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC
The perpendicular from A on side BC of a Δ ABC meets BC at D such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2.
O is a point on side PQ of a APQR such that PO = QO = RO, then ______.
If the perimeter of two similar triangles is in the ratio 2 : 3, what is the ratio of their sides?
If ΔABC ∼ ΔPQR and `(A(ΔABC))/(A(ΔPQR)) = 16/25`, then find AB : PQ.
