Advertisements
Advertisements
प्रश्न
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
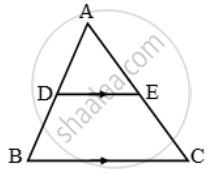
उत्तर
∆ADE ~ ∆ABC.
`\therefore \frac{ar(\Delta ADE)}{ar(\Delta ABC)}=(DE^2)/(BC^2)=((DE)/(BC))^2=(3/5)^2=9/25`
Let ar (∆ADE) = 9x sq units
Then, ar (∆ABC) = 25x sq units
ar (trap. BCED) = ar (∆ABC) – ar (∆ADE)
= (25x – 9x) = (16x) sq units
`\therefore \frac{ar(\Delta ADE)}{ar(trap.BCED)}=\frac{9x}{16x}=\frac{9}{16}`
APPEARS IN
संबंधित प्रश्न
If ∆ABC ~ ∆DEF such that area of ∆ABC is 16cm2 and the area of ∆DEF is 25cm2 and BC = 2.3 cm. Find the length of EF.
If the areas of two similar triangles are equal, prove that they are congruent.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that: (i) ΔAOB and ΔCOD (ii) If OA = 6 cm, OC = 8 cm,
Find:(a) `("area"(triangleAOB))/("area"(triangleCOD))`
(b) `("area"(triangleAOD))/("area"(triangleCOD))`
The areas of two similar triangles are 100 cm2 and 49 cm2 respectively. If the altitude the bigger triangle is 5 cm, find the corresponding altitude of the other.
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 m, prove that area of ΔAPQ is one- sixteenth of the area of ABC.
Ratio of areas of two similar triangles is 9 : 25. _______ is the ratio of their corresponding sides.
If the perimeter of two similar triangles is in the ratio 2 : 3, what is the ratio of their sides?
In ΔABC, seg DE || side BC. If 2A(ΔADE) = A(⬜ DBCE), find AB : AD and show that BC = `sqrt(3)` DE.
If ΔPQR ∼ ΔABC; PQ = 6 cm, AB = 8 cm and the perimeter of ΔABC is 36 cm, then the perimeter of ΔPQR is ______.
