Advertisements
Advertisements
प्रश्न
The areas of two similar triangles are 100 cm2 and 49 cm2 respectively. If the altitude the bigger triangle is 5 cm, find the corresponding altitude of the other.
उत्तर
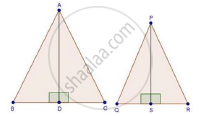
We have, ΔABC ~ ΔPQR
Area(ΔABC) = 100 cm2,
Area (ΔPQR) = 49 cm2
AD = 5 cm
And AD and PS are the altitudes
By area of similar triangle theorem
`("Area"(triangleABC))/("Area"(trianglePQR))="AB"^2/"PQ"^2`
`rArr100/49="AB"^2/"PQ"^2`
`rArr10/7="AB"/"PQ"` ............(i)
In ΔABD and ΔPQS
∠B = ∠Q [ΔABC ~ ΔPQR]
∠ADB = ∠PSQ [Each 90°]
Then, ΔABD ~ ΔPQS [By AA similarity]
`therefore"AB"/"PQ"="AD"/"PS"` .........(ii)[Corresponding parts of similar Δ are proportional]
Compare (i) and (ii)
`"AD"/"PS"=10/7`
`rArr5/"PS"=10/7`
`rArr"PS"=(5xx7)/10=3.5` cm
APPEARS IN
संबंधित प्रश्न
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
Triangles ABC and DEF are similar If AC = 19cm and DF = 8 cm, find the ratio of the area of two triangles.
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that: (i) ΔAOB and ΔCOD (ii) If OA = 6 cm, OC = 8 cm,
Find:(a) `("area"(triangleAOB))/("area"(triangleCOD))`
(b) `("area"(triangleAOD))/("area"(triangleCOD))`
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, find the corresponding median of the other.
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
The perpendicular from A on side BC of a Δ ABC meets BC at D such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2.
In the given figure DE || AC which of the following is true?
In a rectangle Length = 8 cm, Breadth = 6 cm. Then its diagonal = ______.
If ΔABC ~ ΔPQR, AB : PQ = 4 : 5 and A(ΔPQR) = 125 cm2, then find A(ΔABC).
In ΔABC, seg DE || side BC. If 2A(ΔADE) = A(⬜ DBCE), find AB : AD and show that BC = `sqrt(3)` DE.
