Advertisements
Advertisements
Question
The areas of two similar triangles are 100 cm2 and 49 cm2 respectively. If the altitude the bigger triangle is 5 cm, find the corresponding altitude of the other.
Solution
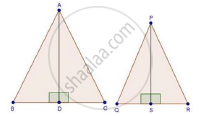
We have, ΔABC ~ ΔPQR
Area(ΔABC) = 100 cm2,
Area (ΔPQR) = 49 cm2
AD = 5 cm
And AD and PS are the altitudes
By area of similar triangle theorem
`("Area"(triangleABC))/("Area"(trianglePQR))="AB"^2/"PQ"^2`
`rArr100/49="AB"^2/"PQ"^2`
`rArr10/7="AB"/"PQ"` ............(i)
In ΔABD and ΔPQS
∠B = ∠Q [ΔABC ~ ΔPQR]
∠ADB = ∠PSQ [Each 90°]
Then, ΔABD ~ ΔPQS [By AA similarity]
`therefore"AB"/"PQ"="AD"/"PS"` .........(ii)[Corresponding parts of similar Δ are proportional]
Compare (i) and (ii)
`"AD"/"PS"=10/7`
`rArr5/"PS"=10/7`
`rArr"PS"=(5xx7)/10=3.5` cm
APPEARS IN
RELATED QUESTIONS
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the area of ΔDEF and ΔABC.
ABC is a triangle in which ∠A =90°, AN⊥ BC, BC = 12 cm and AC = 5cm. Find the ratio of the areas of ΔANC and ΔABC.
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that: (i) ΔAOB and ΔCOD (ii) If OA = 6 cm, OC = 8 cm,
Find:(a) `("area"(triangleAOB))/("area"(triangleCOD))`
(b) `("area"(triangleAOD))/("area"(triangleCOD))`
If ΔABC ~ ΔDEF such that AB = 5 cm, area (ΔABC) = 20 cm2 and area (ΔDEF) = 45 cm2, determine DE.
Prove that in a right-angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
In the adjoining figure, ΔADB ∼ ΔBDC. Prove that BD2 = AD × DC.
If ΔABC ∼ ΔPQR and `(A(ΔABC))/(A(ΔPQR)) = 16/25`, then find AB : PQ.
