Advertisements
Advertisements
Question
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that: (i) ΔAOB and ΔCOD (ii) If OA = 6 cm, OC = 8 cm,
Find:(a) `("area"(triangleAOB))/("area"(triangleCOD))`
(b) `("area"(triangleAOD))/("area"(triangleCOD))`
Solution
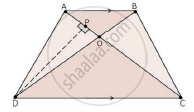
We have,
AB || DC
In ΔAOB and ΔCOD
∠AOB = ∠COD [Vertically opposite angles]
∠OAB = ∠OCD [Alternate interior angles]
Then, ΔAOB ~ ΔCOD [By AA similarity]
(a) By area of similar triangle theorem
`("area"(triangleAOB))/("area"(triangleCOD))="OA"^2/"OC"^2=6^2/8^2=36/64=9/16`
(b) Draw DP ⊥ AC
`therefore("area"(triangleAOD))/("area"(triangleCOD))=(1/2xxAOxxDP)/(1/2xxCOxxDP)`
`="AO"/"CO"=6/8=3/4`
APPEARS IN
RELATED QUESTIONS
If ∆ABC is similar to ∆DEF such that ∆DEF = 64 cm2 , DE = 5.1 cm and area of ∆ABC = 9 cm2 . Determine the area of AB
Let Δ ABC ~ Δ DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC
∆LMN ~ ∆PQR, 9 × A (∆PQR ) = 16 × A (∆LMN). If QR = 20 then Find MN.
In the given figure 1.66, seg PQ || seg DE, A(∆PQF) = 20 units, PF = 2 DP, then Find A(◻DPQE) by completing the following activity.

The perpendicular from A on side BC of a Δ ABC meets BC at D such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2.
If ∆XYZ ~ ∆PQR and A(∆XYZ) = 25 cm2, A(∆PQR) = 4 cm2 then XY : PQ = ?
In the given figure, ΔACB ~ ΔAPQ. If AB = 6 cm, BC = 8 cm, and PQ = 4 cm then AQ is equal to ______.
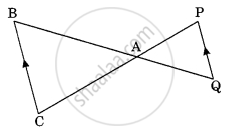
O is a point on side PQ of a APQR such that PO = QO = RO, then ______.
In a rhombus if d1 = 16 cm, d2 = 12 cm, its area will be ______.
Find the length of ST, if ΔPQR ∼ ΔPST.

