Advertisements
Advertisements
Question
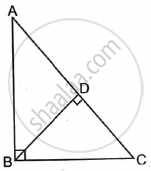
The perpendicular from A on side BC of a Δ ABC meets BC at D such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2.
Solution
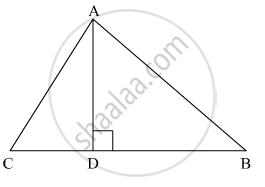
Applying Pythagoras theorem for ΔACD, we obtain
AC2 = AD2 + DC2
AD2 = AC2 - DC2 ......(1)
Applying Pythagoras theorem in ΔABD, we obtain
AB2 = AD2 + DB2
AD2 = AB2 - DB2 .....(2)
From equation (1) and equation (2), we obtain
AC2 - DC2 = AB2 - DB2 .....(3)
It is given that 3DC = DB
∴ `"DC" = "BC"/4` and `"DB"=(3"BC")/ 4`
Putting these values in equation (3), we obtain
`"AC"^2 - ("BC"/4)^2 = "AB"^2 - ((3"BC")/4)^2`
`"AC"^2 - "BC"^2/16 = "AB"^2 - (9"BC"^2)/4`
16AC2 - BC2 = 16AB2 - 9BC2
16AB2 - 16AC2 = 8BC2
2AB2 = 2AC2 + BC2
APPEARS IN
RELATED QUESTIONS
If the areas of two similar triangles are equal, prove that they are congruent.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
In figure below ΔACB ~ ΔAPQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm,
find CA and AQ. Also, find the area (ΔACB): area (ΔAPQ)

Triangles ABC and DEF are similar If AC = 19cm and DF = 8 cm, find the ratio of the area of two triangles.
In Figure, DE || BC If DE = 4cm, BC = 8 cm and Area (ΔADE) = 25 cm2, find the area of ΔABC.
The areas of two similar triangles are 100 cm2 and 49 cm2 respectively. If the altitude the bigger triangle is 5 cm, find the corresponding altitude of the other.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divides ΔABC into two parts equal in area. Find `(BP)/(AB)`
Prove that the points (2, −2), (−2, 1) and (5, 2) are the vertices of a right angled triangle. Also find the area of this triangleb ?
Areas of two similar triangles are 225 sq.cm. 81 sq.cm. If a side of the smaller triangle is 12 cm, then Find corresponding side of the bigger triangle.
In the adjoining figure, ΔADB ∼ ΔBDC. Prove that BD2 = AD × DC.