Advertisements
Advertisements
प्रश्न
The perpendicular from A on side BC of a Δ ABC meets BC at D such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2.
उत्तर
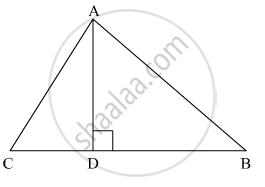
Applying Pythagoras theorem for ΔACD, we obtain
AC2 = AD2 + DC2
AD2 = AC2 - DC2 ......(1)
Applying Pythagoras theorem in ΔABD, we obtain
AB2 = AD2 + DB2
AD2 = AB2 - DB2 .....(2)
From equation (1) and equation (2), we obtain
AC2 - DC2 = AB2 - DB2 .....(3)
It is given that 3DC = DB
∴ `"DC" = "BC"/4` and `"DB"=(3"BC")/ 4`
Putting these values in equation (3), we obtain
`"AC"^2 - ("BC"/4)^2 = "AB"^2 - ((3"BC")/4)^2`
`"AC"^2 - "BC"^2/16 = "AB"^2 - (9"BC"^2)/4`
16AC2 - BC2 = 16AB2 - 9BC2
16AB2 - 16AC2 = 8BC2
2AB2 = 2AC2 + BC2
APPEARS IN
संबंधित प्रश्न
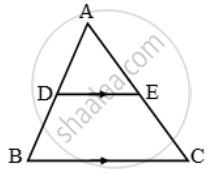
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
Triangles ABC and DEF are similar If AC = 19cm and DF = 8 cm, find the ratio of the area of two triangles.
Triangles ABC and DEF are similar If AB = 1.2 cm and DE = 1.4 cm, find the ratio of the areas of ΔABC and ΔDEF.
The areas of two similar triangles are 81 cm2 and 49 cm2 respectively. Find the ratio of their corresponding heights. What is the ratio of their corresponding medians?
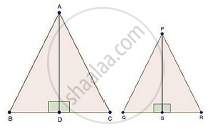
If ΔABC ~ ΔDEF such that AB = 5 cm, area (ΔABC) = 20 cm2 and area (ΔDEF) = 45 cm2, determine DE.
Areas of two similar triangles are 225 sq.cm. 81 sq.cm. If a side of the smaller triangle is 12 cm, then Find corresponding side of the bigger triangle.
In the given figure 1.66, seg PQ || seg DE, A(∆PQF) = 20 units, PF = 2 DP, then Find A(◻DPQE) by completing the following activity.

O is a point on side PQ of a APQR such that PO = QO = RO, then ______.
If ΔABC ~ ΔPQR, AB : PQ = 4 : 5 and A(ΔPQR) = 125 cm2, then find A(ΔABC).
