Advertisements
Advertisements
प्रश्न
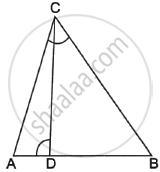
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
उत्तर
Given, ΔABC ∼ ΔPQR
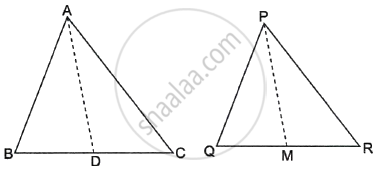
⇒ `("AB")/("PQ") = ("BC")/("QR") = ("AC")/("PR")`
(From the side-ratio property of similar triangles)
⇒ ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R ...(i)
BC = 2BD and QR = 2QM ...(∵ P and M are the midpoints of BC and QR)
⇒ `("AB")/("PQ") = (2 "BD")/(2 "QM") = ("AC")/("PR")`
⇒ `("AB")/("PQ") = ("BD")/("QM") = ("AC")/("PR")` ...(ii)
Now in ΔABD and ΔPQM
`("AB")/("PQ") = ("BD")/("QM")` ...(From (ii))
∠B = ∠Q ...(From (i))
⇒ ΔABD ∼ ΔPQM ...(By SAS similarity criterion)
∴ `("AB")/("PQ") = ("AD")/("PM")`
Hence, proved.
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
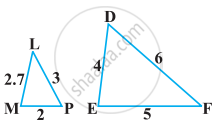
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
In Fig below we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.

The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
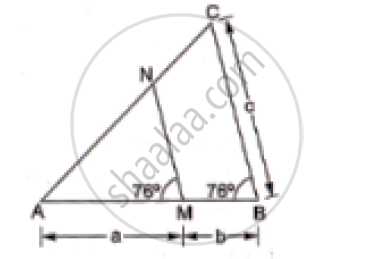
In the given figure, ∠AMN = ∠MBC = 76° . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.
In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.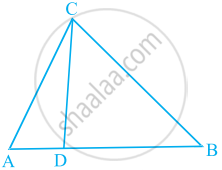
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

In the given figure, ∠ADC = ∠BCA; prove that ΔACB ∼ ΔADC. Hence find BD if AC = 8 cm and AD = 3 cm.