Advertisements
Advertisements
प्रश्न
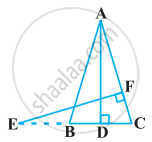
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
उत्तर १
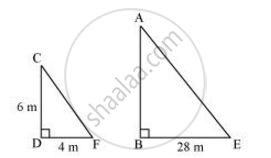
Let AB and CD be a tower and a pole respectively.
Let the shadow of BE and DF be the shadow of AB and CD respectively.
At the same time, the light rays from the sun will fall on the tower and the pole at the same angle.
Therefore, ∠DCF = ∠BAE
And, ∠DFC = ∠BEA
∠CDF = ∠ABE ...(Tower and pole are vertical to the ground)
∴ ΔABE ∼ ΔCDF ...(AAA similarity criterion)
⇒ `("AB")/("CB") = ("BE")/("DF")`
⇒ `("AB")/(6"m") = 28/4`
⇒ AB = 42 m
Therefore, the height of the tower will be 42 metres.
उत्तर २
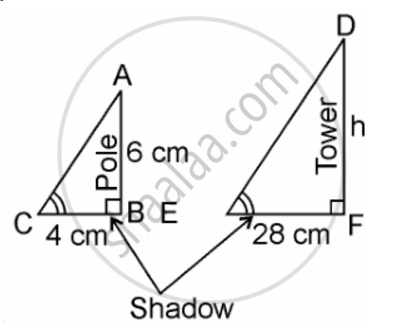
Length of the vertical pole = 6m ...(Given)
Shadow of the pole = 4 m ...(Given)
Let Height of tower = h m
Length of shadow of the tower = 28 m ...(Given)
In ΔABC and ΔDEF,
∠C = ∠E ...(angular elevation of sum)
∠B = ∠F = 90°
∴ ΔABC ~ ΔDEF ...(By AA similarity criterion)
∴ `"AB"/"DF" = "BC"/"EF"` ...(If two triangles are similar corresponding sides are proportional)
∴ `6/h = 4/28`
⇒ `h = (6×28)/4`
⇒ h = 6 × 7
⇒ h = 42 m
Hence, the height of the tower is 42 m.
APPEARS IN
संबंधित प्रश्न
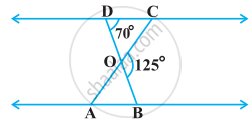
In the following figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
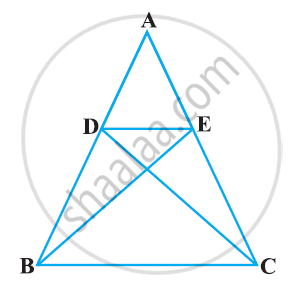
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ∼ ΔECF.
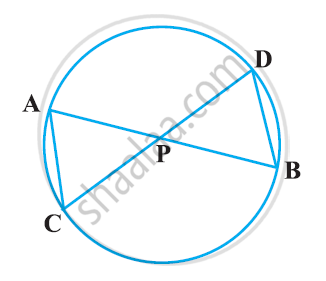
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
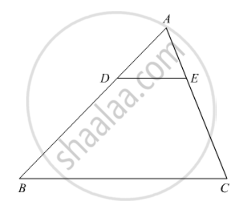
In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
The sides of certain triangles are given below. Determine which of them right triangles are.
1.4cm, 4.8cm, 5cm
In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB) = 84cm2. Find ar(ΔCOD).
The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
Two triangles DEF an GHK are such that ∠D = 48° and ∠H = 57° . If ΔDEF ∼GHK then find the measures of ∠F
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?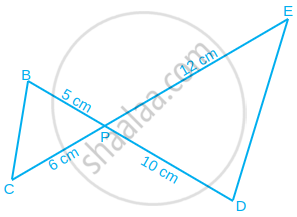
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.