Advertisements
Advertisements
प्रश्न
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
उत्तर
According to the question,
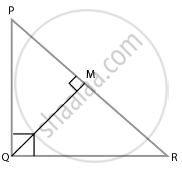
In ∆PQR,
PR2 = QR2 and QM ⊥ PR
Using Pythagoras theorem, we have,
PR2 = PQ2 + QR2
∆PQR is right-angled triangle at Q.
From ∆QMR and ∆PMQ, we have,
∠M = ∠M
∠MQR = ∠QPM ...[= 90° – ∠R]
So, using the AAA similarity criteria,
We have,
∆QMR ∼ ∆PMQ
Also, we know that,
Area of triangles = `1/2` × base × height
So, by property of area of similar triangles,
⇒ `("ar(∆QMR)")/("ar(PMQ)") = ("QM")^2/("PM")^2`
⇒ `("ar(∆QMR)")/("ar(PMQ)") = (1/2 xx "RM" xx "QM")/(1/2 xx "PM" xx "QM")`
⇒ `("ar(∆QMR)")/("ar(PMQ)") = ("QM")^2/("PM")^2`
QM2 = PM × RM
Hence proved.
APPEARS IN
संबंधित प्रश्न
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
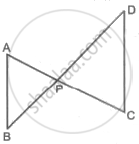
In the above figure, seg AC and seg BD intersect each other in point P. If `("AP")/("CP") = ("BP")/("DP")`, then complete the following activity to prove ΔABP ∼ ΔCDP.
Activity: In ΔABP and ΔCDP
`("AP")/("CP") = ("BP")/("DP")` ......`square`
∴ ∠APB ≅ `square` ......Vertically opposite angles
∴ `square` ∼ ΔCDP ....... `square` test of similarity.
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

