Advertisements
Advertisements
Question
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
Solution
According to the question,
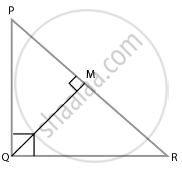
In ∆PQR,
PR2 = QR2 and QM ⊥ PR
Using Pythagoras theorem, we have,
PR2 = PQ2 + QR2
∆PQR is right-angled triangle at Q.
From ∆QMR and ∆PMQ, we have,
∠M = ∠M
∠MQR = ∠QPM ...[= 90° – ∠R]
So, using the AAA similarity criteria,
We have,
∆QMR ∼ ∆PMQ
Also, we know that,
Area of triangles = `1/2` × base × height
So, by property of area of similar triangles,
⇒ `("ar(∆QMR)")/("ar(PMQ)") = ("QM")^2/("PM")^2`
⇒ `("ar(∆QMR)")/("ar(PMQ)") = (1/2 xx "RM" xx "QM")/(1/2 xx "PM" xx "QM")`
⇒ `("ar(∆QMR)")/("ar(PMQ)") = ("QM")^2/("PM")^2`
QM2 = PM × RM
Hence proved.
APPEARS IN
RELATED QUESTIONS
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
In Fig below we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.

The sides of certain triangles are given below. Determine which of them right triangles are.
7cm, 24cm, 25cm
In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.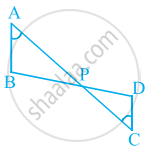
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

