Advertisements
Advertisements
Question
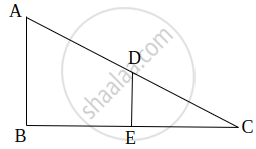
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
Solution
Given that,
`("AB")/("PQ") = ("AC")/("PR") = ("AD")/("PM")`
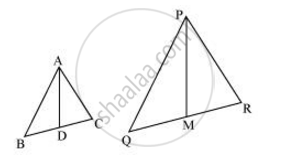
Let us extend AD and PM up to point E and L respectively, such that AD = DE and PM = ML. Then, join B to E, C to E, Q to L, and R to L.
We know that medians divide opposite sides.
Therefore, BD = DC and QM = MR
Also, AD = DE ...(By construction)
And, PM = ML ...(By construction)
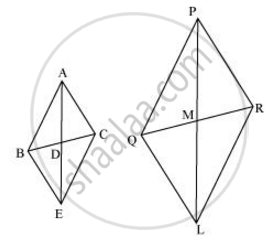
In quadrilateral ABEC, diagonals AE and BC bisect each other at point D.
Therefore, quadrilateral ABEC is a parallelogram.
∴ AC = BE and AB = EC ...(Opposite sides of a parallelogram are equal)
Similarly, we can prove that quadrilateral PQLR is a parallelogram and PR = QL, PQ = LR
It was given that
`("AB")/("PQ") = ("AC")/("PR") = ("AD")/("PM")`
`=>("AB")/("PQ")=("BE")/("QL")= (2"AD")/(2"PM")`
`=>("AB")/("PQ") = ("BE")/("QL") = ("AE")/("PL")`
∴ ΔABE ∼ ΔPQL ...(By SSS similarity criterion)
We know that corresponding angles of similar triangles are equal.
∴ ∠BAE = ∠QPL ...(1)
Similarly, it can be proved that ΔAEC ∼ ΔPLR and
∠CAE = ∠RPL ...(2)
Adding equation (1) and (2), we obtain
∠BAE + ∠CAE = ∠QPL + ∠RPL
⇒ ∠CAB = ∠RPQ ...(3)
In ΔABC and ΔPQR,
`("AB")/("PQ")=("AC")/("PR")`
∠CAB = ∠RPQ ...[Using equation (3)]
∴ ΔABC ∼ ΔPQR ...(By SAS similarity criterion)
APPEARS IN
RELATED QUESTIONS
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
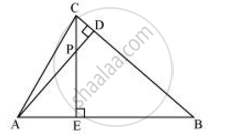
ΔAEP ∼ ΔCDP
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower.
In the following figure, AB || QR. Find the length of PB.

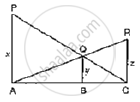
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
In the given figure MN|| BC and AM: MB= 1: 2
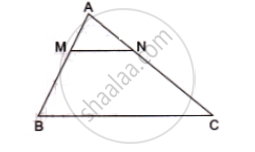
find ` (area(ΔAMN))/(area(ΔABC))`
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

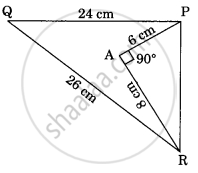
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

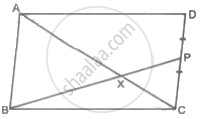
□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC
Which of the following conditions is not sufficient to determine the congruence of two triangles?
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.