English Medium
Academic Year: 2023-2024
Date & Time: 11th March 2024, 10:30 am
Duration: 3h
Advertisements
General Instructions:
Read the following instructions very carefully and strictly follow them:
- This question paper contains 38 questions. All questions are compulsory.
- This question paper is divided into five Sections - A, B, C, D and E.
- In Section-A, Question numbers 1 to 18 are multiple choice questions (MCQs) and question numbers 19 and 20 are Assertion-Reason based questions of 1 mark each.
- In Section B, Question numbers 21 to 25 are very short answer (VSA) type questions, carrying 2 marks each.
- In Section C, Question numbers 26 to 31 are short answer (SA) type questions, carrying 3 marks each.
- In Section D, Question numbers 32 to 35 are long answer (LA) type questions carrying 5 marks each.
- In Section E, Question numbers 36 to 38 are case study based integrated questions carrying 4 marks each. Internal choice is provided in 2 marks question in each case-study.
- There is no overall choice. However, an internal choice has been provided in 2 questions in Section-B, 2 questions in Section-C, 2 questions in Section-D and 3 question in Section-E.
- Draw neat diagrams wherever required. Take `π=22/7` wherever required, if not stated.
- Use of calculators is NOT allowed.
The value of k for which the system of equations 3x − y + 8 = 0 and 6x − ky + 16 = 0 has infinitely many solutions, is ______.
−2
2
`1/2`
`−1/2`
Chapter:
Point P divides the line segment joining the points A(4, –5) and B(1, 2) in the ratio 5:2. Co-ordinates of point P are ______.
`(5/2, (-3)/2)`
`(11/7, 0)`
`(13/7, 0)`
`(0, 13/7)`
Chapter:
The common difference of an A.P. in which a15 − a11 = 48, is ______.
12
16
−12
−16
Chapter:
The quadratic equation x2 + x + 1 = 0 has ______ roots.
Real and Equal
Irrational
Real and distinct
Not-real
Chapter:
If the HCF (2520, 6600) = 40 and LCM (2520, 6600) = 252 × k, then the value of k is ______.
1650
1600
165
1625
Chapter:
In the given figure ΔABC is shown. DE is parallel to BC. If AD = 5 cm, DB = 2.5 cm and BC = 12 cm, then DE is equal to ______.
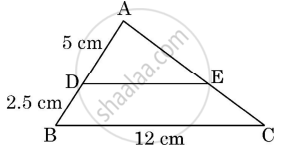
10 cm
6 cm
8 cm
7.5 cm
Chapter:
If sin θ = cos θ, (0° < θ < 90°), then value of (sec θ · sin θ) is ______.
`1/sqrt2`
`sqrt2`
1
0
Chapter:
Two dice are rolled together. The probability of getting the sum of the two numbers to be more than 10, is ______.
`1/9`
`1/6`
`7/12`
`1/12`
Chapter:
If α and β are zeroes of the polynomial 5x2 + 3x − 7, the value of `1/α + 1/β` is ______.
`-3/7`
`3/5`
`3/7`
`-5/7`
Chapter:
The perimeters of two similar triangles ABC and PQR are 56 cm and 48 cm respectively. PQ/AB is equal to ______.
`7/8`
`6/7`
`7/6`
`8/7`
Chapter:
AB and CD are two chords of a circle intersecting at P. Choose the correct statement from the following:
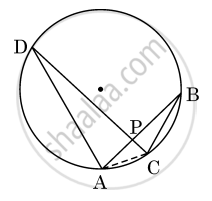
ΔADP ~ ΔCBA
ΔADP ~ ΔBPC
ΔADP ~ ΔBCP
ΔADP ~ ΔCBP
Chapter:
If value of each observation in a data is increased by 2, then median of the new data ______.
increases by 2
increases by 2n
remains same
decreases by 2
Chapter:
A box contains cards numbered 6 to 55. A card is drawn at random from the box. The probability that the drawn card has a number which is a perfect square, is ______.
`7/50`
`7/55`
`1/10`
`5/49`
Chapter:
In the given figure, tangents PA and PB to the circle centred at O, from point P are perpendicular to each other. If PA = 5 cm, then length of AB is equal to ______.
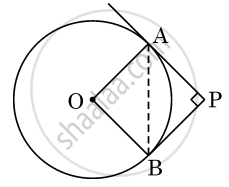
5 cm
`5sqrt2` cm
`2sqrt5` cm
10 cm
Chapter:
XOYZ is a rectangle with vertices X(-3, 0), O(0, 0), Y(0, 4) and Z(x, y). The length of its each diagonal is ______.
5 units
`sqrt5` units
x2 + y2 units
4 units
Chapter:
Which term of the A.P. −29, −26, −23, ....., 61 is 16?
11th
16th
10th
31th
Chapter:
Advertisements
In the given figure, AT is tangent to a circle centred at O. If ∠CAT = 40°, then ∠CBA is equal to ______.
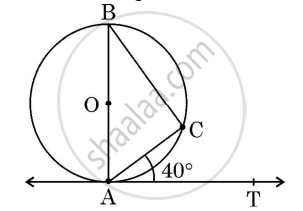
70°
50°
65°
40°
Chapter:
After an examination, a teacher wants to know the marks obtained by maximum number of the students in her class. She requires to calculate ______ of marks.
Median
Mode
Mean
Range
Chapter:
Assertion (A): If sin A `1/3` (0° < A < 90°), then the value of cos A is `(2sqrt2)/3`.
Reason (R): For every angle θ, sin2θ + cos2θ = 1.
Both Assertion (A) and Reason (R) are true. Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true. Reason (R) does not give correct explanation of (A).
Assertion (A) is true but Reason (R) is not true.
Assertion (A) is not true but Reason (R) is true.
Chapter:
Assertion (A): Two cubes each of edge length 10 cm are joined together.
The total surface area of newly formed cuboid is 1200 cm2.
Reason (R): Area of each surface of a cube of side 10 cm is 100 cm2.
Both Assertion (A) and Reason (R) are true. Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true. Reason (R) does not give correct explanation of (A).
Assertion (A) is true but Reason (R) is not true.
Assertion (A) is not true but Reason (R) is true.
Chapter:
Can the number (15)n, n being a natural number, end with the digit 0? Give reasons.
Chapter:
Find the type of triangle ABC formed whose vertices are A(1, 0), B(−5, 0) and C(−2, 5).
Chapter:
If 2 sin (A + B) = `sqrt3` and cos (A − B) = 1, then find the measures of angles A and B. 0 ≤ A, B, (A + B) ≤ 90°.
Chapter:
In the given figure, AB and CD are tangents to a circle centred at O. Is ∠BAC = ∠DCA? Justify your answer.
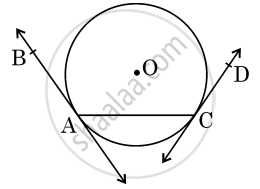
Chapter:
In what ratio is the line segment joining the points (3, −5) and (−1, 6) divided by the line y = x?
Chapter:
A(3, 0), B(6, 4) and C(−1, 3) are vertices of a triangle ABC. Find length of its median BE.
Chapter:
If the sum of first m terms of an A.P. is same as sum of its first n terms (m ≠ n), then show that the sum of its first (m + n) terms is zero.
Chapter:
In a A.P., the sum of the three consecutive terms is 24 and the sum of their squares is 194. Find the numbers.
Chapter:
Advertisements
Prove that `sqrt(5)` is an irrational number.
Chapter: [0.011000000000000001] Real Numbers
In the given figure, PQ is tangent to a circle centred at O and ∠BAQ = 30°, show that BP = BQ.
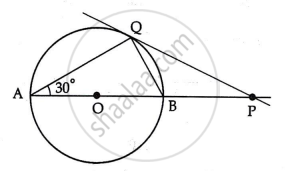
Chapter:
In the given figure, AB, BC, CD and DA are tangents to the circle with centre O forming a quadrilateral ABCD.
Show that ∠AOB + ∠COD = 180°
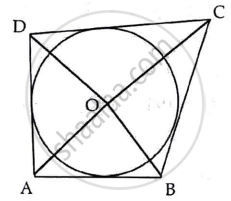
Chapter:
Prove that `(1 + sec θ - tan θ)/(1 + sec θ + tan θ) = (1 - sin θ)/(cos θ)`.
Chapter:
In a test, the marks obtained by 100 students (out of 50) are given below:
| Marks obtained: | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Number of students: | 12 | 23 | 34 | 25 | 6 |
Find the mean marks of the students.
Chapter:
In a 2-digit number, the digit at the unit's place is 5 less than the digit at the ten's place. The product of the digits is 36. Find the number.
Chapter:
Using graphical method, solve the following system of equations:
3x + y + 4 = 0 and 3x − y + 2 = 0
Chapter:
Tara scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each wrong answer, then Tara would have scored 50 marks. Assuming that Tara attempted all question, find the total number of questions in the test.
Chapter:
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then prove that the other two sides are divided in the same ratio.
Chapter:
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
Chapter: [0.040999999999999995] Triangles
From the top of a 45 m high light house, the angles of depression of two ships, on the opposite side of it, are observed to be 30° and 60°. If the line joining the ships passes through the foot of the light house, find the distance between the ships. (Use `sqrt3` =1.73)
Chapter:
The perimeter of a certain sector of a circle of radius 5.6 m is 20.0 m. Find the area of the sector.
Chapter:
A ball is thrown in the air so that t seconds after it is thrown, its height h metre above its starting point is given by the polynomial h = 25t − 5t2.
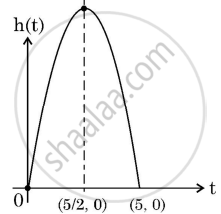
Observe the graph of the polynomial and answer the following questions:
- Write zeroes of the given polynomial. [1]
- Find the maximum height achieved by ball. [1]
- After throwing upward, how much time did the ball take to reach to the height of 30 m? [2]
OR - Find the two different values of t when the height of the ball was 20 m. [2]
- After throwing upward, how much time did the ball take to reach to the height of 30 m? [2]
Chapter:
The word ‘circus’ has the same root as ‘circle’. In a closed circular area, various entertainment acts including human skill and animal training are presented before the crowd.
A circus tent is cylindrical upto a height of 8 m and conical above it. The diameter of the base is 28 m and total height of tent is 18.5 m.

Based on the above, answer the following questions:
- Find slant height of the conical part. [1]
- Determine the floor area of the tent. [1]
- Find area of the cloth used for making tent. [2]
OR - Find total volume of air inside an empty tent. [2]
- Find area of the cloth used for making tent. [2]
Chapter:
In a survey on holidays, 120 people were asked to state which type of transport they used on their last holiday. The following pie chart shows the results of the survey.
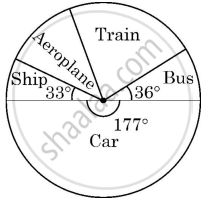
Observe the pie chart and answer the following questions:
- If one person is selected at random, find the probability that he/she travelled by bus or ship.
- Which is most favourite mode of transport and how many people used it?
- A person is selected at random. If the probability that he did not use train is 4/5, find the number of people who used train.
OR - The probability that randomly selected person used aeroplane is 7/60. Find the revenue collected by air company at the rate of ₹ 5,000 per person.
- A person is selected at random. If the probability that he did not use train is 4/5, find the number of people who used train.
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2023 - 2024
Previous year Question paper for CBSE Class 10 Maths-2024 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
