Advertisements
Advertisements
Question
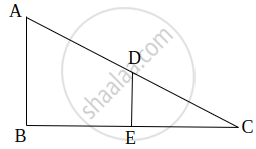
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
Solution
According to the question,
AC and PQ intersect each other at the point O and AB || DC.
From ∆AOP and ∆COQ,
∠AOP = ∠COQ ...[Since they are vertically opposite angles]
∠APO = ∠CQO ...[Since, AB || DC and PQ is transversal, the angles are alternate angles]
∴ ∆AOP ∼ ∆COQ ...[Using AAA similarity criterion]
Then, since, corresponding sides are proportional
We have,
`("OA")/("OC") = ("AP")/("CQ")`
OA × CQ = OC × AP
Hence proved.
APPEARS IN
RELATED QUESTIONS
In below figure, ∠A = ∠CED, Prove that ΔCAB ~ ΔCED. Also, find the value of x.
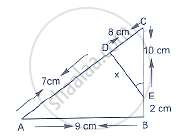
In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
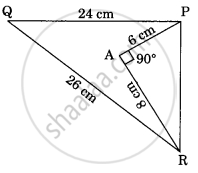
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

Which of the following is NOT a similarity criterion of traingles?
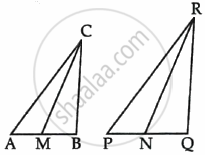
In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ∼ ΔPQR, then prove that ΔAMC ∼ ΔPNR.
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.