Advertisements
Advertisements
Question
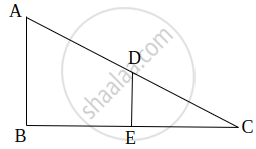
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.
Options
`("ac")/"b"`
`("ac")/("b" + "c")`
`("ab")/"c"`
`("ab")/("b" + "c")`
Solution
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is `underlinebb((ac)/(b + c))`

Explanation:
In ΔCDE and ΔCAB
∠C = ∠C ...[Common]
∠1 = ∠2 ...[Corresponding angles as DE || AB]
ΔCDE ∼ ΔCAB ...[By AA rule]
`("DE")/("AB") = ("CE")/("BC")` ...[Sides of similar triangles]
`x/"a" = "c"/("b" + "c")`
x = `("ac")/("b" + "c")`
APPEARS IN
RELATED QUESTIONS
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ∼ ΔECF.
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

