Advertisements
Advertisements
Question
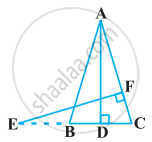
In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ∼ ΔECF.
Solution
Given: ∆ABC in which AB = AC and AD ⊥ BC. Side CB is produced to E and EF ⊥ AC.
To prove ∆ABD ~ ∆ECF,
Proof: we know that the angles opposite to equal sides of a triangle are equal.
∠B = ∠C ...[∵ AB = AC]
Now, in ∆ABD and ∆ECF, we have
∴ ∠B = ∠C ...[proved above]
∠ADB = ∠EFC = 90°
∴ ∆ABD ~ ∆ECF ...[By AA-similarity]
APPEARS IN
RELATED QUESTIONS
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
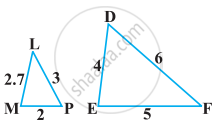
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

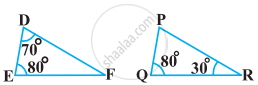
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
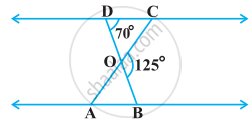
In the following figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
In ΔABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that:
(i) ΔOMA and ΔOLC
(ii) `"OA"/"OC"="OM"/"OL"`
The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
In the given figure MN|| BC and AM: MB= 1: 2
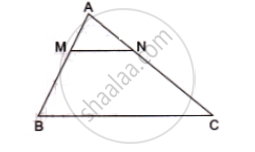
find ` (area(ΔAMN))/(area(ΔABC))`
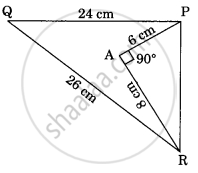
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
Which of the following conditions is not sufficient to determine the congruence of two triangles?
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

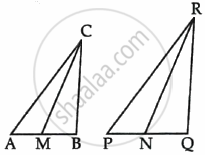
In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ∼ ΔPQR, then prove that ΔAMC ∼ ΔPNR.
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
