Advertisements
Advertisements
Question
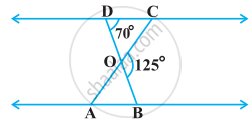
In the following figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
Solution
DOB is a straight line.
∴ ∠DOC + ∠COB = 180°
⇒ ∠DOC = 180° − 125°
⇒ ∠DOC = 55°
In ΔDOC,
∠DCO + ∠CDO + ∠DOC = 180°
(Sum of the measures of the angles of a triangle is 180°.)
⇒ ∠DCO + 70° + 55° = 180°
⇒ ∠DCO = 55°
It is given that ΔODC ∼ ΔOBA
∴ ∠OAB = ∠OCD ...[Corresponding angles are equal in similar triangles.]
⇒ ∠OAB = 55°
APPEARS IN
RELATED QUESTIONS
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
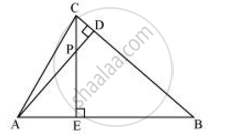
ΔAEP ∼ ΔCDP
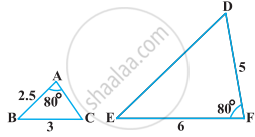
In the following figure, AB || QR. Find the length of PB.

In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
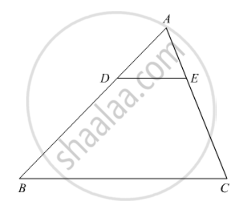
In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
The sides of certain triangles are given below. Determine which of them right triangles are.
7cm, 24cm, 25cm
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

In the given figure, value of x(in cm) is

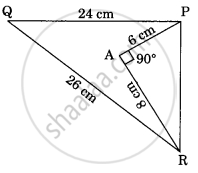
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
In the figure, if DE∥BC, AD = 3cm, BD = 4cm and BC= 14 cm, then DE equals ______.
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
In figure, ABC is a triangle right angled at B and BD ⊥ AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.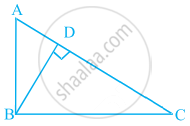
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?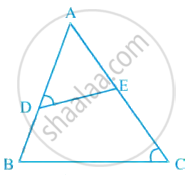
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
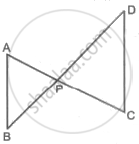
In the above figure, seg AC and seg BD intersect each other in point P. If `("AP")/("CP") = ("BP")/("DP")`, then complete the following activity to prove ΔABP ∼ ΔCDP.
Activity: In ΔABP and ΔCDP
`("AP")/("CP") = ("BP")/("DP")` ......`square`
∴ ∠APB ≅ `square` ......Vertically opposite angles
∴ `square` ∼ ΔCDP ....... `square` test of similarity.
Which of the following is NOT a similarity criterion of traingles?
`square`ABCD is trapezium, AB || CD diagonals of trapezium intersects in point P.
Write the answers of the following questions:
- Draw the figure using the given information.
- Write any one pair of alternate angles and opposite angles.
- Write the names of similar triangles with the test of similarity.
