Advertisements
Advertisements
Question
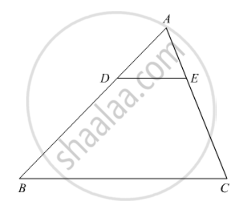
In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
Solution
We have, DE || BC, AB = 6 cm and AE `= 1/4` AC
In ΔADE and ΔABC
∠A = ∠A [Common]
∠ADE = ∠ABC [Corresponding angles]
Then, ΔADE ~ ΔABC [By AA similarity]
`rArr"AD"/"AB"="AE"/"AC"` [Corresponding parts of similar Δ are proportional]
`rArr"AD"/6=(1/4AC)/"AC"` [∵ AE `=1/4` AC given]
`"AD"/6=1/4`
`rArr"AD"=6/4=1.5` cm
APPEARS IN
RELATED QUESTIONS
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
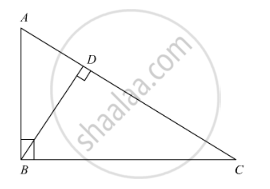
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm, find BC.
In Fig below we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.

In the given figure MN|| BC and AM: MB= 1: 2
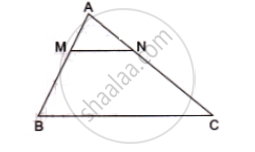
find ` (area(ΔAMN))/(area(ΔABC))`
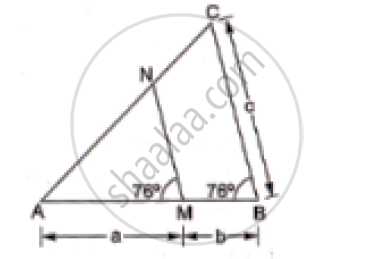
In the given figure, ∠AMN = ∠MBC = 76° . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
If ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal ______.
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.