Advertisements
Advertisements
Question
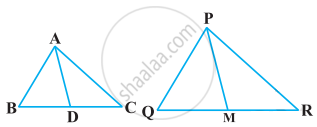
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.
Solution
We have MBC and PQR in which AD and PM are medians corresponding to sides BC and QR respectively such that
`("AB")/("PQ") = ("BC")/("QR") = ("AD")/("PM")`
`("AB")/("PQ") = (1/2 "BC")/(1/2 "QR") = ("AD")/("PM")`
`("AB")/("PQ") = ("BD")/("QM") = ("AD")/("PM")`
Using SSS similarity, we have
ΔABD ~ ΔPQM
Their corresponding angles are equal.
∠ABD = ∠PQM
∠ABC = ∠PQR
Now, in MBC and ΔPQR,
`("AB")/("PQ") = ("BC")/("QR")` ...[1]
Also, ∠ABC = ∠PQR ...[2]
From [1] and [2]
ΔABC ~ ΔPQR ...[SAS similarity]
RELATED QUESTIONS
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ∼ ΔECF.
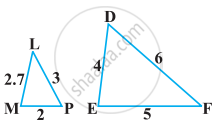
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
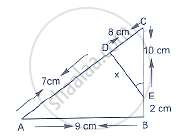
In below figure, ∠A = ∠CED, Prove that ΔCAB ~ ΔCED. Also, find the value of x.
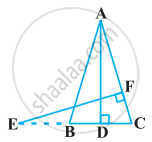
D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
Two triangles DEF an GHK are such that ∠D = 48° and ∠H = 57° . If ΔDEF ∼GHK then find the measures of ∠F
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.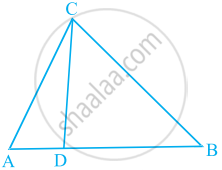
In figure, ABC is a triangle right angled at B and BD ⊥ AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.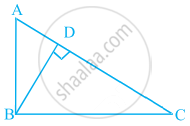
Which of the following conditions is not sufficient to determine the congruence of two triangles?
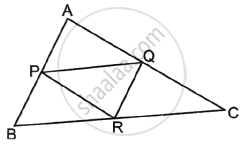
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
