Advertisements
Advertisements
Question
In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
Solution 1
(i) In ΔABC and ΔAMP,
∠ABC = ∠AMP ...(Each 90°)
∠A = ∠A ...(Common)
∴ ΔABC ∼ ΔAMP ...(By AA similarity criterion)
(ii) We have,
∠B = ∠M = 90°
And, ∠BAC = ∠MAP
In ΔABC and ΔAMP
∠B = ∠M ...[Each 90°]
∠BAC = ∠MAP ...[Given]
Then, ΔABC ~ ΔAMP ....[By AA similarity]
∴ `"CA"/"PA"="BC"/"MP"` ....[Corresponding parts of similar Δ are proportional.]
Solution 2
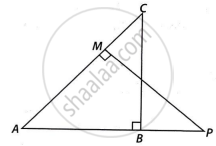
We have,
∠B = ∠M = 90°
And, ∠BAC = ∠MAP
In ΔABC and ΔAMP
∠B = ∠M ...[Each 90°]
∠BAC = ∠MAP ...[Given]
Then, ΔABC ~ ΔAMP ...[By AA similarity]
∴ `"CA"/"PA"="BC"/"MP"` ....[Corresponding parts of similar Δ are proportional]
APPEARS IN
RELATED QUESTIONS
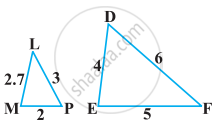
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
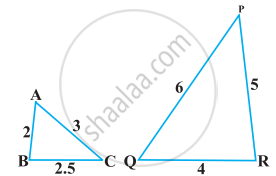
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
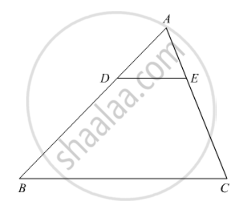
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
The sides of certain triangles are given below. Determine which of them right triangles are.
1.4cm, 4.8cm, 5cm
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
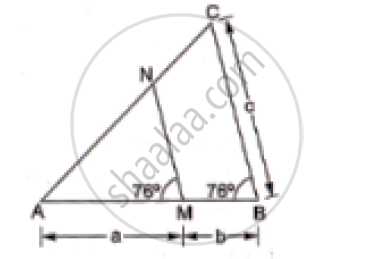
In the given figure, ∠AMN = ∠MBC = 76° . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?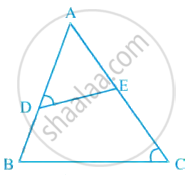
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
