Advertisements
Advertisements
Question
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
Solution
Let A be the position of the street bulb fixed on a pole AB = 6 m and CD = 1.5 m be the height of a woman and her shadow be ED = 3 m.
Let distance between pole and woman be x m.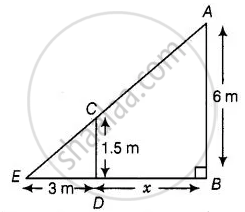
Here, woman and pole both are standing vertically.
So, CD || AB
In ΔCDE and ΔABE,
∠E = ∠E ...[Common angle]
∠ABE = ∠CDE ...[Each equal to 90°]
∴ ΔCDE ∼ ΔABE ...[By AAA similarity criterion]
Then, `("ED")/("EB") = ("CD")/("AB")`
⇒ `3/(3 + x) = 1.5/6`
⇒ 3 × 6 = 1.5(3 + x)
⇒ 18 = 1.5 × 3 + 1.5x
⇒ 1.5 = 18 – 4.5
∴ x = `(13.5)/1.5` = 9 m
Hence, she is at the distance of 9 m from the base of the pole.
APPEARS IN
RELATED QUESTIONS
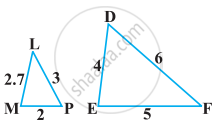
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
The sides of certain triangles are given below. Determine which of them right triangles are.
7cm, 24cm, 25cm
State the AAA-similarity criterion
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
Two triangles DEF an GHK are such that ∠D = 48° and ∠H = 57° . If ΔDEF ∼GHK then find the measures of ∠F
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?
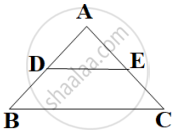
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

