Advertisements
Advertisements
प्रश्न
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
उत्तर
Let A be the position of the street bulb fixed on a pole AB = 6 m and CD = 1.5 m be the height of a woman and her shadow be ED = 3 m.
Let distance between pole and woman be x m.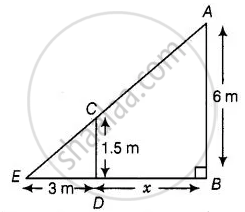
Here, woman and pole both are standing vertically.
So, CD || AB
In ΔCDE and ΔABE,
∠E = ∠E ...[Common angle]
∠ABE = ∠CDE ...[Each equal to 90°]
∴ ΔCDE ∼ ΔABE ...[By AAA similarity criterion]
Then, `("ED")/("EB") = ("CD")/("AB")`
⇒ `3/(3 + x) = 1.5/6`
⇒ 3 × 6 = 1.5(3 + x)
⇒ 18 = 1.5 × 3 + 1.5x
⇒ 1.5 = 18 – 4.5
∴ x = `(13.5)/1.5` = 9 m
Hence, she is at the distance of 9 m from the base of the pole.
APPEARS IN
संबंधित प्रश्न
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
State the two properties which are necessary for given two triangles to be similar.
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
In the given figure, value of x(in cm) is

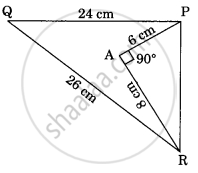
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.