Advertisements
Advertisements
प्रश्न
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
उत्तर
Let BC = 18 m be the flag pole and its shadow be AB = 9.6 m.
The distance of the top of the pole, C from the far end i.e., A of the shadow is AC.
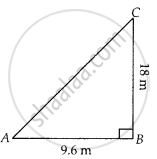
In right angled ∆ABC,
AC2 = AB2 + BC2 ...[By pythagoras theorem]
⇒ AC2 = (9.6)2 + (18)2
⇒ AC2 = 92.16 + 324
⇒ AC2 = 416.16
∴ AC = `sqrt(416.16)` = 20.4 m
Hence, the required distance is 20.4 m.
APPEARS IN
संबंधित प्रश्न
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD

Find the Pythagorean triplet from among the following set of numbers.
4, 5, 6
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
