Advertisements
Advertisements
प्रश्न
In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD

उत्तर
Given : AC = 12 m
BD = 9 m
PA = PB= 15 m
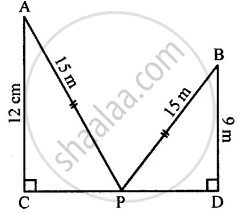
(i) In right angle triangle ACP
(AP)2 = (AC)2 + (CP)2
152 = 122 + CP2
225 = 144 + CP2
225 – 144 = CP2
81 = CP
`sqrt81` = CP
∴ CP = 9 m
(ii) In right angle triangle BPD
(PB)2 = (BD)2 + (PD)2
(15)2 = (9)2 + PD2
225 = 81 + PD2
225 – 81 = PD2
144 = PD2
`sqrt144` = PD2
∴ PD = 12 m
(iii) CP = 9 m
PD = 12 m
∴ CD = CP + PD
= 9 + 12
= 21 m
APPEARS IN
संबंधित प्रश्न
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

In ∆ABC, seg AD ⊥ seg BC, DB = 3CD.
Prove that: 2AB2 = 2AC2 + BC2

In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2`
In the given figure, PQ = `"RS"/(3)` = 8cm, 3ST = 4QT = 48cm.
SHow that ∠RTP = 90°.
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
