Advertisements
Advertisements
प्रश्न
In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
उत्तर
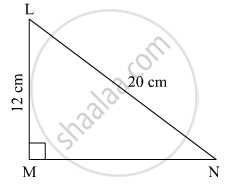
In the right-angled triangle LMN, ∠M = 90°. Hence, side LN is the hypotenuse.
According to Pythagoras' theorem,
l(LN)2 = l(MN)2 + l(LM)2
⇒ (20)2 = l(MN)2 + (12)2
⇒ 400 = l(MN)2 + 144
⇒ l(MN)2 = 400 − 144
⇒ l(MN)2 = 256
⇒ l(MN)2 = (16)2
⇒ l(MN) = 16
∴ Length of seg MN = 16 cm.
संबंधित प्रश्न
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 13 cm, 12 cm, 5 cm
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
In a trapezium ABCD, seg AB || seg DC seg BD ⊥ seg AD, seg AC ⊥ seg BC, If AD = 15, BC = 15 and AB = 25. Find A(▢ABCD)

In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
The length of the diagonals of rhombus are 24cm and 10cm. Find each side of the rhombus.
In the given figure, PQ = `"RS"/(3)` = 8cm, 3ST = 4QT = 48cm.
SHow that ∠RTP = 90°.
If ‘l‘ and ‘m’ are the legs and ‘n’ is the hypotenuse of a right angled triangle then, l2 = ________
