Question

In a trapezium ABCD, seg AB || seg DC seg BD ⊥ seg AD, seg AC ⊥ seg BC, If AD = 15, BC = 15 and AB = 25. Find A(▢ABCD)

Answer 1

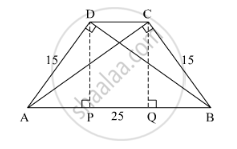
According to Pythagoras theorem,
In ∆ADB

\[{AB}^2 = {AD}^2 + {DB}^2 \]
\[ \Rightarrow \left( 25 \right)^2 = \left( 15 \right)^2 + {BD}^2 \]
\[ \Rightarrow 625 = 225 + {BD}^2 \]
\[ \Rightarrow {BD}^2 = 625 - 225\]
\[ \Rightarrow {BD}^2 = 400\]
\[ \Rightarrow BD = 20\]

Now,

A (ΔADB) = `1/2 xx "base" xx "height"`

= `1/2 xx "AD" xx "BD"`

= `1/2 xx 15 xx 20`

= 150 sq. units
 Also, 
\[\text{Area of the triangle} = \frac{1}{2} \times \text{base} \times \text{height}\]
\[ \Rightarrow 150 = \frac{1}{2} \times 25 \times DP\]
\[ \Rightarrow DP = \frac{300}{25}\]
\[ \Rightarrow DP = 12\]

Therefore, height of the trapezium = 12.

Now,
According to Pythagoras theorem,
In ∆ADP

\[{AD}^2 = {AP}^2 + {DP}^2 \]
\[ \Rightarrow \left( 15 \right)^2 = \left( 12 \right)^2 + {AP}^2 \]
\[ \Rightarrow 225 = 144 + {AP}^2 \]
\[ \Rightarrow {AP}^2 = 225 - 144\]
\[ \Rightarrow {AP}^2 = 81\]
\[ \Rightarrow AP = 9\]

∴ AP = QB = 9

∴ CD = PQ

AB = AP + PQ + BQ   ...(∵ A-P-Q-B)

25 = 9 + PQ + 9

25 = 18 + PQ

 25 − 18 = PQ

PQ = 7

In ▢ DPQC,

DC || PQ    ...(∵ AB || DC)

DP || CQ    ...(perpendicular to same lines are parallel)

∴ ▢ DPQC is a parallogram.

∴ CD = PQ = 7   ...(∵ Opposite sides of parallelogram)

\[\text{Area of Trapezium} = \frac{1}{2} \times \text{Sum of parallel sides} \times \text{Height}\]
\[ = \frac{1}{2} \times \left( 25 + 7 \right) \times 12\]
\[ = \frac{1}{2} \times 32 \times 12\]
\[ = 32 \times 6\]
 = 192 sq . units

Hence, A(▢ABCD) = 192 sq. units.