Advertisements
Advertisements
प्रश्न
In a trapezium ABCD, seg AB || seg DC seg BD ⊥ seg AD, seg AC ⊥ seg BC, If AD = 15, BC = 15 and AB = 25. Find A(▢ABCD)

उत्तर
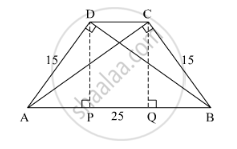
According to Pythagoras theorem,
In ∆ADB
\[{AB}^2 = {AD}^2 + {DB}^2 \]
\[ \Rightarrow \left( 25 \right)^2 = \left( 15 \right)^2 + {BD}^2 \]
\[ \Rightarrow 625 = 225 + {BD}^2 \]
\[ \Rightarrow {BD}^2 = 625 - 225\]
\[ \Rightarrow {BD}^2 = 400\]
\[ \Rightarrow BD = 20\]
Now,
Also,
\[\text{Area of the triangle} = \frac{1}{2} \times \text{base} \times \text{height}\]
\[ \Rightarrow 150 = \frac{1}{2} \times 25 \times DP\]
\[ \Rightarrow DP = \frac{300}{25}\]
\[ \Rightarrow DP = 12\]
According to Pythagoras theorem,
In ∆ADP
\[ \Rightarrow \left( 15 \right)^2 = \left( 12 \right)^2 + {AP}^2 \]
\[ \Rightarrow 225 = 144 + {AP}^2 \]
\[ \Rightarrow {AP}^2 = 225 - 144\]
\[ \Rightarrow {AP}^2 = 81\]
\[ \Rightarrow AP = 9\]
\[ = \frac{1}{2} \times \left( 25 + 7 \right) \times 12\]
\[ = \frac{1}{2} \times 32 \times 12\]
\[ = 32 \times 6\]
= 192 sq . units
Hence, A(▢ABCD) = 192 sq. units.
संबंधित प्रश्न
Side of a triangle is given, determine it is a right triangle.
`(2a – 1) cm, 2\sqrt { 2a } cm, and (2a + 1) cm`
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, ho much string does she have out (see Figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
In the right-angled ∆PQR, ∠ P = 90°. If l(PQ) = 24 cm and l(PR) = 10 cm, find the length of seg QR.
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
