Advertisements
Advertisements
प्रश्न
In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
उत्तर १
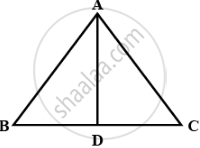
In equilateral Δ ABC, AD ⊥ BC.
Therefore, BC = x cm.
Area of equilateral ΔABC = `sqrt3/4 xx "side"^2 = 1/2 xx "base" xx "height"`
= `sqrt3/4 xx x^2 = 1/2 xx x xx "AD"`
AD = `sqrt3/2 x`
उत्तर २
In △ADC and △ADB,
AD = AD ...(Common)
∠ADB = ∠ADC ...(Each 90°)
AB = AC ....(Given, ABC is an equilateral triangle)
Thus, △ADC ≅ △ADB
BD = DC = `1/2`BC ...(By cpct)
Hence, BD = `1/2`x
In △ADB,
∠D = 90°
△ADB is right angle triangle,
by Pythagoras theorem,
AB2 = BD2 + AD2
`x^2 = (1/2x)^2 + "AD"^2`
`"AD"^2 = x^2 − (x^2)/4`
`"AD"^2 = 3/4x^2`
`"AD" = (sqrt(3))/2x`
APPEARS IN
संबंधित प्रश्न
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 13 cm, 12 cm, 5 cm
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD
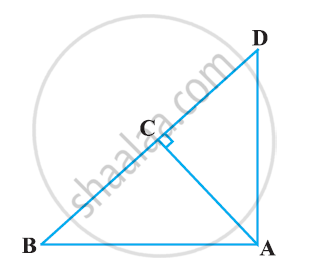
In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.
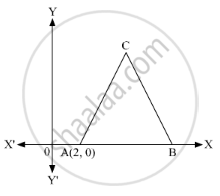
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?
Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
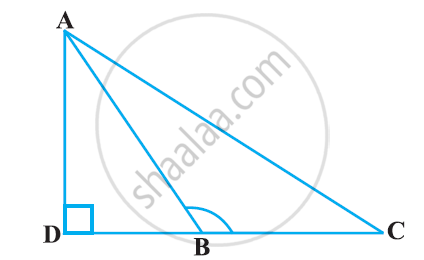
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
Find the value of (sin2 33 + sin2 57°)
From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
Find the length of the support cable required to support the tower with the floor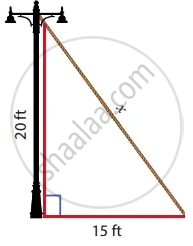
In the figure, find AR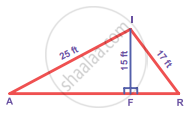
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.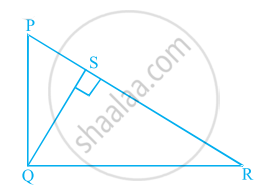
Two angles are said to be ______, if they have equal measures.
Two squares are congruent, if they have same ______.
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
