Advertisements
Advertisements
Question
In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
Solution 1
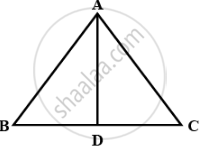
In equilateral Δ ABC, AD ⊥ BC.
Therefore, BC = x cm.
Area of equilateral ΔABC = `sqrt3/4 xx "side"^2 = 1/2 xx "base" xx "height"`
= `sqrt3/4 xx x^2 = 1/2 xx x xx "AD"`
AD = `sqrt3/2 x`
Solution 2
In △ADC and △ADB,
AD = AD ...(Common)
∠ADB = ∠ADC ...(Each 90°)
AB = AC ....(Given, ABC is an equilateral triangle)
Thus, △ADC ≅ △ADB
BD = DC = `1/2`BC ...(By cpct)
Hence, BD = `1/2`x
In △ADB,
∠D = 90°
△ADB is right angle triangle,
by Pythagoras theorem,
AB2 = BD2 + AD2
`x^2 = (1/2x)^2 + "AD"^2`
`"AD"^2 = x^2 − (x^2)/4`
`"AD"^2 = 3/4x^2`
`"AD" = (sqrt(3))/2x`
APPEARS IN
RELATED QUESTIONS
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 13 cm, 12 cm, 5 cm
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD . Prove that 2AB2 = 2AC2 + BC2.

Which of the following can be the sides of a right triangle?
1.5 cm, 2 cm, 2.5 cm
In the case of right-angled triangles, identify the right angles.
Identify, with reason, if the following is a Pythagorean triplet.
(24, 70, 74)
In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.
Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
In ΔABC, if DE || BC, AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then value of x is ______.
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a – b) = (c + d)(c – d).
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
In a triangle, sum of squares of two sides is equal to the square of the third side.
