Advertisements
Advertisements
Question
In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a – b) = (c + d)(c – d).
Solution
Given: In ∆PQR,
PD ⊥ QR,
PQ = a,
PR = b,
QD = c
And DR = d
To prove: (a + b)(a – b) = (c + d)(c – d)
Proof: In right angled ΔPDQ,
PQ2 = PD2 + QD2 ...[By pythagoras theorem]
⇒ a2 = PD2 + c2
⇒ PD2 = a2 – c2 ...(i)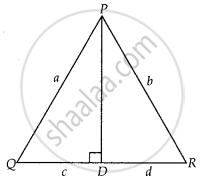
In right angled ∆PDR,
PR2 = PD2 + DR2 ...[By pythagoras theorem]
⇒ b2 = PD2 + d2
⇒ PD2 = b2 – d2 ...(ii)
From equations (i) and (ii),
a2 – c2 = b2 – d2
⇒ a2 – b2 = c2 – d2
⇒ (a – b)(a + b) = (c – d)(c + d)
Hence proved.
APPEARS IN
RELATED QUESTIONS
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.

A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
