Advertisements
Advertisements
Question
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

Solution
Here, we first need to join OA, OB, and OC after which the figure becomes as follows,
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides. First, we consider the ΔARO and applying Pythagoras theorem we get,
AQ2 = AR2 + OR2
AR2 = AQ2 - OR2 ...(i)
Similarly, from triangles, BPO, COQ, AOQ, CPO, and BRO we get the following results,
BP2 = BO2 - OP2 ...(ii)
CQ2 = OC2 - OQ2 ...(iii)
AQ2 = AO2 - OQ2 ...(iv)
CP2 = OC2 - OP2 ...(v)
BR2 = OB2 - OR2 ...(vi)
Adding (i), (ii) and (iii), we get
AR2 + BP2 + CQ2 = AQ2 - OR2 + BO2 - OP2 + OC2 - OQ2 ...(vii)
Adding (iv), (v) and (vi), we get,
AQ2 + CP2 + BR2 = AO2 - OR2 + BO2 - OP2 + OC2 - OQ2 ...(viii)
From (vii) and (viii), we get,
AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2
Hence, proved.
APPEARS IN
RELATED QUESTIONS
In Figure ABD is a triangle right angled at A and AC ⊥ BD. Show that AC2 = BC × DC

ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
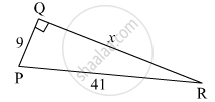
In the figure below, find the value of 'x'.
Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
In a right angled triangle, the hypotenuse is the greatest side
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
The longest side of a right angled triangle is called its ______.
Two angles are said to be ______, if they have equal measures.
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
