Advertisements
Advertisements
Question
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
Advertisements
Solution
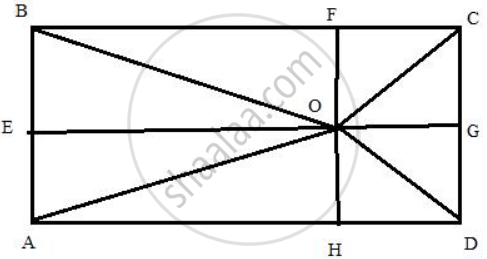
Draw rectangle ABCD with arbitrary point O within it, and then draw lines OA, OB, OC, OD. Then draw lines from point O perpendicular to the sides: OE, OF, OG, OH.
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Using Pythagorean theorem we have from the above diagram:
OA2 = AH2 + OH2 = AH2 + AE2
OC2 = CG2 + OG2 = EB2 + HD2
OB2 = EO2 + BE2 = AH2 + BE2
OD2 = HD2 + OH2 = HD2 + AE2
Adding these equalities we get:
OA2 + OC2 = AH2 + HD2 + AE2 + EB2
OB2 + OD2 = AH2 + HD2 + AE2 + EB2
From which we prove that for any point within the rectangle there is the relation
OA2 + OC2 = OB2 + OD2
Hence Proved.
APPEARS IN
RELATED QUESTIONS
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
The sides of the triangle are given below. Find out which one is the right-angled triangle?
40, 20, 30
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 - AB2 = 2BC x ED
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
In a triangle, sum of squares of two sides is equal to the square of the third side.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
