Advertisements
Advertisements
Question
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution
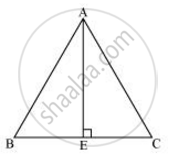
Let the side of the equilateral triangle be a, and AE be the altitude of ΔABC.
`:. BE = EC = (BC)/2 = a/2`
Applying Pythagoras theorem in ΔABE, we obtain
AB2 = AE2 + BE2
`a^2 = AE^2 + (a/2)^2`
`AE^2 = a^2 - a^2/4`
`AE^2 = (3a^2)/4`
4AE2 = 3a2
⇒ 4 × (Square of altitude) = 3 × (Square of one side)
APPEARS IN
RELATED QUESTIONS
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
(A)\[7 + \sqrt{5}\]
(B) 5
(C) 10
(D) 12
Identify, with reason, if the following is a Pythagorean triplet.
(4, 9, 12)
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9AQ2 = 9AC2 + 4BC2
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
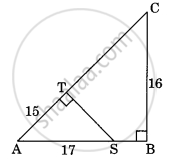
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
