Advertisements
Advertisements
प्रश्न
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
उत्तर
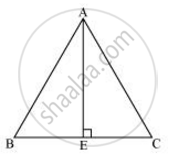
Let the side of the equilateral triangle be a, and AE be the altitude of ΔABC.
`:. BE = EC = (BC)/2 = a/2`
Applying Pythagoras theorem in ΔABE, we obtain
AB2 = AE2 + BE2
`a^2 = AE^2 + (a/2)^2`
`AE^2 = a^2 - a^2/4`
`AE^2 = (3a^2)/4`
4AE2 = 3a2
⇒ 4 × (Square of altitude) = 3 × (Square of one side)
APPEARS IN
संबंधित प्रश्न
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
For finding AB and BC with the help of information given in the figure, complete following activity.
AB = BC .......... 
∴ ∠BAC = 
∴ AB = BC =  × AC
× AC
=  × `sqrt8`
× `sqrt8`
=  × `2sqrt2`
× `2sqrt2`
= 

In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
In a right angled triangle, the hypotenuse is the greatest side
Find the length of the support cable required to support the tower with the floor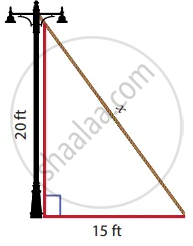
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
