Advertisements
Advertisements
प्रश्न
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
उत्तर
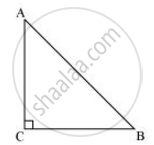
Given that ΔABC is an isosceles triangle.
∴ AC = CB
Applying Pythagoras theorem in ΔABC (i.e., right-angled at point C), we obtain
AC2 + CB2 = AB2
=> AC2+ AC2 = AB2 (AC = CB)
⇒ 2AC2 = AB2
APPEARS IN
संबंधित प्रश्न
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
Find the unknown side in the following triangles
Find the distance between the helicopter and the ship
