Advertisements
Advertisements
प्रश्न
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
उत्तर
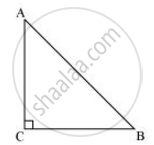
Given that ΔABC is an isosceles triangle.
∴ AC = CB
Applying Pythagoras theorem in ΔABC (i.e., right-angled at point C), we obtain
AC2 + CB2 = AB2
=> AC2+ AC2 = AB2 (AC = CB)
⇒ 2AC2 = AB2
APPEARS IN
संबंधित प्रश्न
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
In the right-angled ∆PQR, ∠ P = 90°. If l(PQ) = 24 cm and l(PR) = 10 cm, find the length of seg QR.
A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
