Advertisements
Advertisements
प्रश्न
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
उत्तर
Let AC be the ladder of length 5 m and BC = 4 m be the height of the wall, which ladder is placed.
If the foot of the ladder is moved 1.6 m towards the wall i.e, AD = 1.6 m,
Then the ladder is slide upward i.e., CE = x m.
In right angled ∆ABC,
AC2 = AB2 + BC2 ...[By pythagoras theorem]
⇒ (5)2 = (AB)2 + (4)2
⇒ AB2 = 25 – 16 = 9
⇒ AB = 3 m
Now, DB = AB – AD
= 3 – 1.6
= 1.4 m
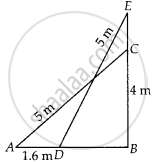
In right angled ∆EBD,
ED2 = EB2 + BD2 ...[By pythagoras theorem]
⇒ (5)2 = (EB)2 + (14)2 ...[BD = 1.4]
⇒ 25 = (EB)2 + 1.96
⇒ (EB)2 = 25 – 1.96 = 23.04
⇒ EB = `sqrt(23.04)` = 4.8
Now, EC = EB – BC
= 4.8 – 4
= 0.8
Hence, the top of the ladder would slide upwards on the wall at distance is 0.8 m.
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, ho much string does she have out (see Figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
For finding AB and BC with the help of information given in the figure, complete following activity.
AB = BC .......... 
∴ ∠BAC = 
∴ AB = BC =  × AC
× AC
=  × `sqrt8`
× `sqrt8`
=  × `2sqrt2`
× `2sqrt2`
= 

Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
A right-angled triangle may have all sides equal.
