Question

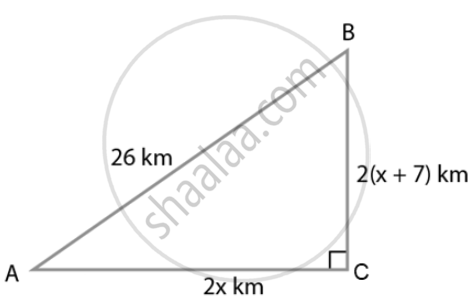
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.

Answer 1

According to the question,

AC ⊥ CB,

AC = 2x km,

CB = 2(x + 7) km

And AB = 26 km

Thus, we get ∆ACB right angled at C.

Now, from ∆ACB,

Using Pythagoras Theorem,

AB² = AC² + BC²

⇒ (26)² = (2x)² + {2(x + 7)}²

⇒ 676 = 4x² + 4(x² + 196 + 14x)

⇒ 676 = 4x² + 4x² + 196 + 56x

⇒ 676 = 8² + 56x + 196

⇒ 8x² + 56x – 480 = 0

Dividing the equation by 8, we get,

x² + 7x – 60 = 0

x² + 12x – 5x – 60 = 0

x(x + 12) – 5(x + 12) = 0

(x + 12)(x – 5) = 0

∴ x = –12 or x = 5

Since the distance can’t be negative, we neglect x = –12

∴ x = 5

Now,

AC = 2x = 10 km

BC = 2(x + 7)

= 2(5 + 7)

= 24 km

Thus, the distance covered to city B from city A via city C = AC + BC

AC + BC = 10 + 24

= 34 km

Distance covered to city B from city A after the highway was constructed = BA = 26 km

Therefore, the distance saved = 34 – 26 = 8 km.