Advertisements
Advertisements
Question
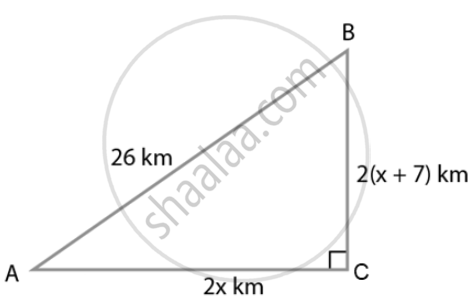
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
Solution
According to the question,
AC ⊥ CB,
AC = 2x km,
CB = 2(x + 7) km
And AB = 26 km
Thus, we get ∆ACB right angled at C.
Now, from ∆ACB,
Using Pythagoras Theorem,
AB2 = AC2 + BC2
⇒ (26)2 = (2x)2 + {2(x + 7)}2
⇒ 676 = 4x2 + 4(x2 + 196 + 14x)
⇒ 676 = 4x2 + 4x2 + 196 + 56x
⇒ 676 = 82 + 56x + 196
⇒ 8x2 + 56x – 480 = 0
Dividing the equation by 8, we get,
x2 + 7x – 60 = 0
x2 + 12x – 5x – 60 = 0
x(x + 12) – 5(x + 12) = 0
(x + 12)(x – 5) = 0
∴ x = –12 or x = 5
Since the distance can’t be negative, we neglect x = –12
∴ x = 5
Now,
AC = 2x = 10 km
BC = 2(x + 7)
= 2(5 + 7)
= 24 km
Thus, the distance covered to city B from city A via city C = AC + BC
AC + BC = 10 + 24
= 34 km
Distance covered to city B from city A after the highway was constructed = BA = 26 km
Therefore, the distance saved = 34 – 26 = 8 km.
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm;
find the length of side BC.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
The longest side of a right angled triangle is called its ______.
A right-angled triangle may have all sides equal.
