Advertisements
Advertisements
Question
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
Solution

Let side of equilateral triangle be a. And AE be the altitude of ΔABC
So, BE = EC = `"BC"/(2) = "a"/(2)`
And, AE = `("a"sqrt(3))/(2)`
Given that BD = `(1)/(3)"BC" = "a"/(3)`
So, DE = BD - BE = `"a"/(2) - "a"/(3) = "a"/(6)`
Now, in ΔADE by applying Pythagoras theorem
AD2 = AE2 + DE2
AD2 = `(("a"sqrt(3))/(2))^2 + ("a"/6)^2`
= `((3"a"^2)/4) + ("a"^2/36) = (28"a"^2)/(36)`
Or, 9 AD2 = 7 AB2.
APPEARS IN
RELATED QUESTIONS
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
In a ∆ABC, AD ⊥ BC and AD2 = BC × CD. Prove ∆ABC is a right triangle
Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.
AD is drawn perpendicular to base BC of an equilateral triangle ABC. Given BC = 10 cm, find the length of AD, correct to 1 place of decimal.
In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
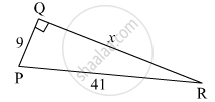
In the figure below, find the value of 'x'.
Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 - AB2 = 2BC x ED
In the given figure, PQ = `"RS"/(3)` = 8cm, 3ST = 4QT = 48cm.
SHow that ∠RTP = 90°.
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
In a right angled triangle, the hypotenuse is the greatest side
In the figure, find AR
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
In an isosceles triangle PQR, the length of equal sides PQ and PR is 13 cm and base QR is 10 cm. Find the length of perpendicular bisector drawn from vertex P to side QR.
The longest side of a right angled triangle is called its ______.
