Advertisements
Advertisements
Question
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
Solution
L.H.S = `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2`
=`(sin^2 θ + cosec^2 θ + 2 sin θ cosec θ + cos^2 θ + sec^2 θ + 2 cos θ sec θ)`
=`(sin^2 θ +cos^2 θ) + (cosec^2 θ + sec^2 θ) + 2sin θ (1/sin θ) + 2 cos θ (1/cos θ)`
= `(1) + (1 + cot^2 θ + 1 + tan^2 θ) + (2) + (2)`
= `7 + tan^2 θ + cot^2 θ`
= R .H. S
APPEARS IN
RELATED QUESTIONS
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD . Prove that 2AB2 = 2AC2 + BC2.

ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

The sides of the triangle are given below. Find out which one is the right-angled triangle?
40, 20, 30
In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
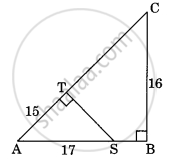
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
Two circles having same circumference are congruent.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
