Advertisements
Advertisements
Question
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
Solution
Let the height of the top be x m.
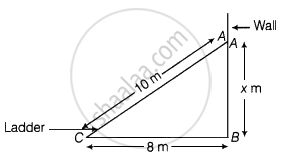
In right angled ΔACB,
AC2 = AB2 + BC2 .....[By Pythagoras theorem]
⇒ AB2 + AC2 – BC2
⇒ x2 = (10)2 – (8)2 = 100 – 84
⇒ x = `sqrt(36)`
⇒ x = 6 m
Hence, the height of the top is 6 m.
APPEARS IN
RELATED QUESTIONS
Which of the following can be the sides of a right triangle?
1.5 cm, 2 cm, 2.5 cm
In the case of right-angled triangles, identify the right angles.
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

In the figure below, find the value of 'x'.

Find the Pythagorean triplet from among the following set of numbers.
3, 4, 5
Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
