Advertisements
Advertisements
Question
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
Solution
Let the length of the ladder be x m.
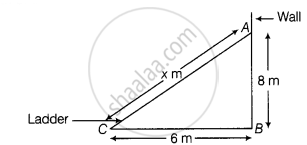
In right angled ΔABC,
AC2 = AB2 + BC2 ......[By Pythagoras theorem]
⇒ (x)2 = (8)2 + (6)2
⇒ `sqrt((8)^2 + (6)^2)` = `sqrt(64 + 36)` = `sqrt(100)`
⇒ x = 10 m
Hence, the length of the ladder is 10 m.
APPEARS IN
RELATED QUESTIONS
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD . Prove that 2AB2 = 2AC2 + BC2.

In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that:
4(BL2 + CM2) = 5 BC2

In the figure: ∠PSQ = 90o, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
In the right-angled ∆PQR, ∠ P = 90°. If l(PQ) = 24 cm and l(PR) = 10 cm, find the length of seg QR.
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is __________
