Advertisements
Advertisements
प्रश्न
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
उत्तर
Let the height of the top be x m.
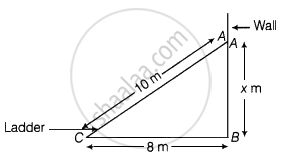
In right angled ΔACB,
AC2 = AB2 + BC2 .....[By Pythagoras theorem]
⇒ AB2 + AC2 – BC2
⇒ x2 = (10)2 – (8)2 = 100 – 84
⇒ x = `sqrt(36)`
⇒ x = 6 m
Hence, the height of the top is 6 m.
APPEARS IN
संबंधित प्रश्न
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
From the given figure, in ∆ABQ, if AQ = 8 cm, then AB =?

The longest side of a right angled triangle is called its ______.
