Advertisements
Advertisements
प्रश्न
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
Advertisements
उत्तर
The pictorial form of the given problem is as follows:
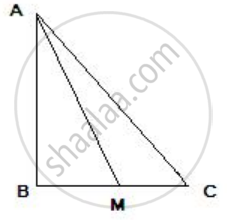
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
First, we consider the ΔABM and applying Pythagoras theorem we get,
AM2 = AB2 + BM2
AB2 = AM2 - BM2 ...(i)
Now, we consider the ΔABC and applying Pythagoras theorem we get,
AC2 = AB2 + BC2
AB2 = AC2 - BC2 ...(ii)
From (i) and (ii) we get,
AM2 - BM2 = AC2 - BC2
AM2 + BC2 = AC2 + BM2
Hence, Proved.
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
In a right triangle ABC right-angled at C, P and Q are the points on the sides CA and CB respectively, which divide these sides in the ratio 2 : 1. Prove that
`(i) 9 AQ^2 = 9 AC^2 + 4 BC^2`
`(ii) 9 BP^2 = 9 BC^2 + 4 AC^2`
`(iii) 9 (AQ^2 + BP^2 ) = 13 AB^2`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:
`"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
In the following figure, AD is perpendicular to BC and D divides BC in the ratio 1: 3.
Prove that : 2AC2 = 2AB2 + BC2
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.
From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
From given figure, In ∆ABC, If AC = 12 cm. then AB =?
Activity: From given figure, In ∆ABC, ∠ABC = 90°, ∠ACB = 30°
∴ ∠BAC = `square`
∴ ∆ABC is 30° – 60° – 90° triangle
∴ In ∆ABC by property of 30° – 60° – 90° triangle.
∴ AB = `1/2` AC and `square` = `sqrt(3)/2` AC
∴ `square` = `1/2 xx 12` and BC = `sqrt(3)/2 xx 12`
∴ `square` = 6 and BC = `6sqrt(3)`
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:
(i) `"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
(ii) `"AB"^2 = "AD"^2 - "BC"."DM" + (("BC")/2)^2`
(iii) `"AC"^2 + "AB"^2 = 2"AD"^2 + 1/2"BC"^2`
Points A and B are on the opposite edges of a pond as shown in the following figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.
