Advertisements
Advertisements
प्रश्न
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of `(20 "km")/"hr"` and the second train travels at `(30 "km")/"hr"`. After 2 hours, what is the distance between them?
उत्तर
A is the position of the 1st train.
B is the position of the 2nd train.
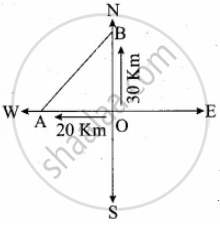
Distance Covered in 2 hours
OA = 2 × 20 = 40 km
OB = 2 × 30 = 60 km
Distance between the train after 2 hours
AB = `sqrt("OA"^2 + "OB"^2)`
= `sqrt(40^2 + 60^2)`
= `sqrt(1600 + 3600)`
= `sqrt(5200)` or `sqrt(52 xx 100)`
= `10sqrt(4 xx 13)`
= `20sqrt(13)`
= 72.11 km
Distance between the two train = 72.11 km or `20sqrt(13) "km"`
APPEARS IN
संबंधित प्रश्न
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
In an isosceles triangle, length of the congruent sides is 13 cm and its base is 10 cm. Find the distance between the vertex opposite the base and the centroid.
In the figure: ∠PSQ = 90o, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is __________
