Advertisements
Advertisements
प्रश्न
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 = `"p"^2 + "a"x + "a"^2/4`
उत्तर
Given ∠AED = 90°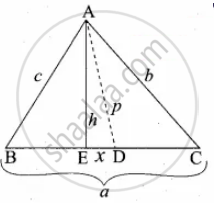
ED = x, DC = `"a"/2` ...(D is the mid point of BC)
∴ EC = `x + "a"/2`, BE = `"a"/2 - x`
∴ In the right ∆AED
AD2 = AE2 + ED2
p2 = h2 + x2
In the right ∆AEC,
AC2 = AE2 + EC2
b2 = `"h"^2 + (x + "a"/2)^2`
= `"h"^2 + x^2 + "a"^2/4 + 2 xx x xx "a"/2`
b2 = `"p"^2 + "a"^2/4 + "a"x`
b2 = `"p"^2 + "a"x + 1/4 "a"^2`
APPEARS IN
संबंधित प्रश्न
In figure, ∠A = ∠CED, prove that ∆CAB ~ ∆CED. Also, find the value of x.

In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
- Prove that ΔACD is similar to ΔBCA.
- Find BC and CD.
- Find area of ΔACD : area of ΔABC.

A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2 PD

Construct a ΔABC in which CA = 6 cm, AB = 5 cm and ∠BAC = 45°. Then construct a triangle whose sides are `3/5` of the corresponding sides of ΔABC.
In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
PR = 26 cm, QR = 24 cm, ∠PAQ = 90°, PA = 6 cm and QA = 8 cm. Find ∠PQR
Write the test of similarity for triangles given in figure.
