Question

D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c² = `"p"^2 - "a"x + "a"^2/4`

Answer 1

From the figure, D is the midpoint of BC.

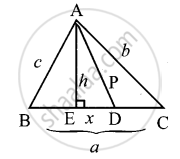
We have ∠AED = 90°

∴ ∠ADE < 90° and ∠ADC > 90°

i.e. ∠ADE is acute and ∠ADC is obtuse,

In ∆ABD, ∠ADE is an acute angle.

AB² = AD² + BD² – 2BD . DE

⇒ AB² = AD² + (12BC)2 – 2 × 12 BC . DE

⇒ AB² = AD² + 14 BC² – BC . DE

⇒ AB² = AD² – BC . DE + 14 BC²

⇒ c² = p² – ax + 14 a²

Hence proved.