Advertisements
Advertisements
प्रश्न
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c2 = `"p"^2 - "a"x + "a"^2/4`
उत्तर
From the figure, D is the midpoint of BC.
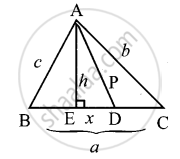
We have ∠AED = 90°
∴ ∠ADE < 90° and ∠ADC > 90°
i.e. ∠ADE is acute and ∠ADC is obtuse,
In ∆ABD, ∠ADE is an acute angle.
AB2 = AD2 + BD2 – 2BD . DE
⇒ AB2 = AD2 + (12BC)2 – 2 × 12 BC . DE
⇒ AB2 = AD2 + 14 BC2 – BC . DE
⇒ AB2 = AD2 – BC . DE + 14 BC2
⇒ c2 = p2 – ax + 14 a2
Hence proved.
APPEARS IN
संबंधित प्रश्न
Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
A vertical stick 20 cm long casts a shadow 6 cm long on the ground. At the same time, a tower casts a shadow 15 m long on the ground. Find the height of the tower.
See the given figure. DE || BC. Find AD.

ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
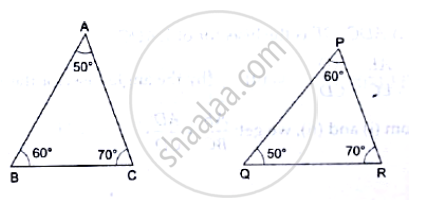
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
On a map drawn to a scale of 1 : 25000, a rectangular plot of land, ABCD is measured as AB= 12 cm and BC = 16cm. calculate the diagonal distance of the plot in km and the plot area in km2 .
Through the vertex S of a parallelogram PQRS, a line is drawn to intersect the sides Qp and QR produced at M and N respectively. Prove that `"SP"/"PM" = "MQ"/"QN" = "MR"/"SR"`
ΔXYZ is enlarged to ΔX'Y'Z'. If XY = 12cm, YZ = 8cm and XZ = 14cm and the smallest side of ΔX'Y'Z' is 12cm, find the scale factor and use it to find the length of the other sides of the image ΔX'Y'Z'.
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
In figure, if AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm and ∠ADE = 48°. Find ∠ABC.

